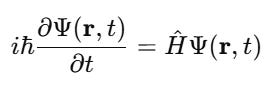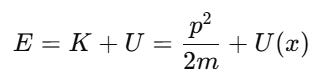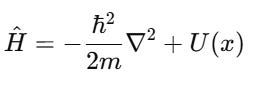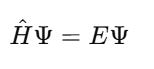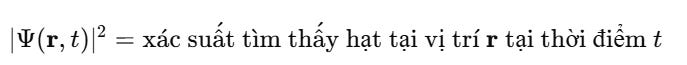Schrodinger
phương trình Schrödinger là trái tim của cơ học lượng tử, tương tự như định luật Newton trong cơ học cổ điển.
Nói ngắn gọn, nó mô tả cách trạng thái lượng tử của một hệ (ví dụ: electron) thay đổi theo thời gian và không gian.
🧠 1. Dạng tổng quát của phương trình Schrödinger:
Trong đó:
Ký hiệu Ý nghĩa Ψ(r,t) Hàm sóng – mô tả trạng thái lượng tử của hạt (vị trí, năng lượng, xác suất…)
i Đơn vị ảo
ℏ Hằng số Planck rút gọn
H^ Toán tử Hamilton – biểu diễn tổng năng lượng của hệ (động năng + thế năng)
⚙️ 2. Trong cơ học cổ điển:
Ta có:
Trong cơ học lượng tử, thay vì dùng đại lượng số học, ta dùng toán tử:
📘 3. Dạng đứng yên (stationary Schrödinger equation)
Khi hệ không thay đổi theo thời gian (năng lượng không đổi):
→ Đây là phương trình giá trị riêng (eigenvalue equation).
Nghiệm của nó cho ta:
Ψn: hàm sóng ứng với trạng thái lượng tử thứ n
En: mức năng lượng rời rạc tương ứng
Chính điều này giải thích tại sao năng lượng của electron trong nguyên tử bị lượng tử hóa (chỉ nhận các giá trị rời rạc).
🌌 4. Ý nghĩa vật lý của hàm sóng Ψ\PsiΨ
Bản thân Ψ\PsiΨ không phải là xác suất, nhưng:
Đây là nội dung xác suất của cơ học lượng tử – khác hẳn tư duy xác định của Newton.
🔍 5. Ví dụ quen thuộc:
Đối với nguyên tử hydro, giải phương trình Schrödinger sẽ cho ra:
Các mức năng lượng rời rạc (giống mô hình Bohr, nhưng chính xác hơn),
Và các orbital (hàm sóng 3D) như 1s,2s,2p,3d,…1s, 2s, 2p, 3d, \dots1s,2s,2p,3d,…
Nếu bạn muốn, mình có thể vẽ hình minh họa trực quan cho phương trình Schrödinger của nguyên tử hydro (các orbital và mức năng lượng) — bạn có muốn mình vẽ không?